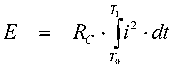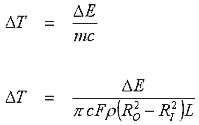|
Coil Power Handling If you intend to build a high power coilgun then you must give consideration to the amount of resistive dissipation which will occur in the coil during a firing sequence. The instantaneous power dissipation in the coil is given by the product of the square of the current and the coils resistance
and the total energy converted to heat is given by the integral of the power dissipation function.
where T0 and T1 are the start and stop times of the current waveform. If you intend to make reasonably accurate calculations of the heat energy generated then you'll need to know something about the shape of the current waveform, that means recording it using a DSO.
Now let's look at the actual temperature change which comes from the dissipation. Typical current pulses in a coilgun are of the order of a few ms or less so negligible heat energy will dissipate to the air during a pulse and we can assume that all the resistive energy losses will go into heating the coil. The standard equation relating the change in thermal energy of a body to its change in temperature is
where m is the mass and c is the specific heat capacity. We can express the mass of the coil in terms of its parameters as follows
where We can now combine these equations and express the temperature change in the coil as a function of the energy dissipated.
Values of density
and specific heat capacity for copper are; The largest temperature rise which can be accomodated depends on the insulation rating of the wire. Typically this is around 1250C so taking a ambient temperature of say 250C means that the temperature change in the coil is limited to an absolute maximum of 1000C. Now it makes sense to stay on the safe of this so limiting the rise to about 750C is a safe bet. If you melt the insulation the coil will be ruined. It's possible to get wire with a higher insulation temperature rating. The time required for cooling between firings is a more complicated issue from the point of view of calculations. Some of the more obvious factors are the thermal mass of the coil, the surface area of the coil, and the heat transfer to the coil matrix material. The matrix is the material between the windings of the coil. In a low field coil this can simply be air, but if additional mechanical strength is required then the coil may be impregnated with a resin, or bound with glass fibre tape between layers and then impregnated. This analysis is simplified by ignoring phenomenon such as the skin and proximity effects. A more detailed analysis of the issues surrounding the thermal analysis of pulsed coils can be found in Principles of Pulsed Magnet Design by R. Kratz and P. Wyder. Sources:
|
is the density of the wire material and F is the filling factor.
