|
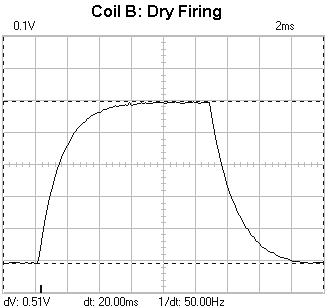
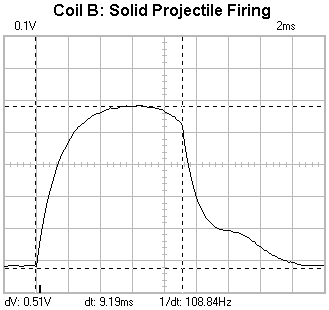
Open Loop Pulse Triggering Results Coil B Fig 1 illustrates the dry firing for coil B. The voltage markers give a dV of 0.51V resulting in a wire current of 51A. Coil B data shows the wire diameter as 1.0mm so the wire and coil current densities are 64.9Amm-1 and 51Amm-1 respectively. Note that this is larger than the densities calculated for coil A. Fig 2 shows the current waveform resulting from firing a projectile.
Fig 1. Coil current during dry firing
Fig 2. Projectile interaction with coil
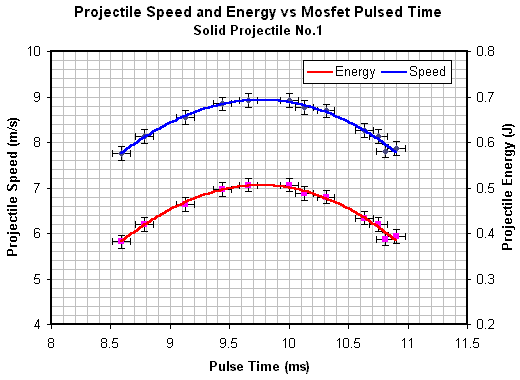
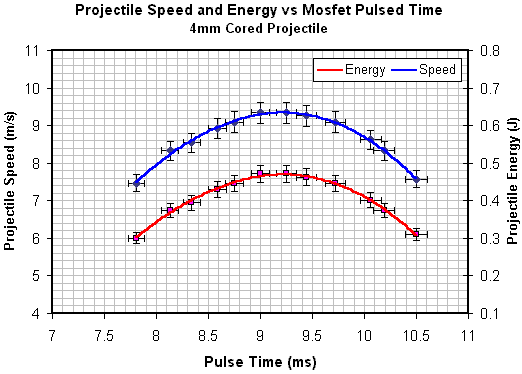
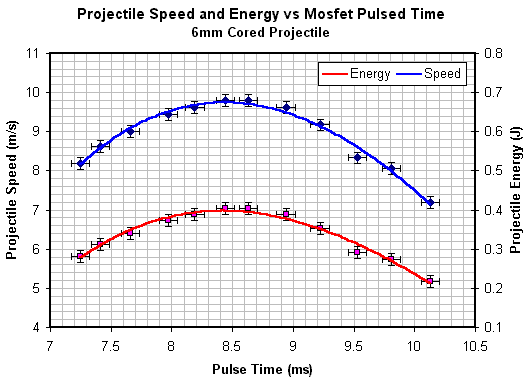
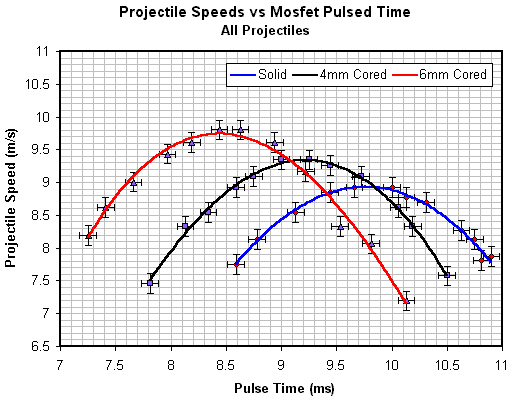
The specific shape of the modified current waveform depends on when the current pulse is terminated. The shape in fig 2 is typical of current pulses close to the optimal length. Fig 3 - 5 illustrate the projectile speed and energy characteristics. Fig 6 plots the three projectile speed curves for comparison.
Fig 3. Solid projectile No. 1 speed and energy data
Fig 4. 4mm cored projectile speed and energy data
Fig 5. 6mm cored projectile speed and energy data
Fig 6. Projectile Speed Comparison
Coil Efficiency Using the same data processing techniques as described in the results from coil A we can determine the efficiency of coil B. The data is tabulated below.
Table 1. Energy and efficiency data
It's still not clear if there is really any distinguishable difference in coil efficiency with different projectiles. One thing you may have noticed is that I haven't included and error value with the coil losses. The reason for this is that I don't know what the error is likely to be from the integrations. I suppose I could guesstimate a value of, say, 5% but it's not really important at the moment. I would certainly argue that the efficiency of coil B is greater than that of coil A. Finally we can see that the peak power is close to double that of coil A, it's quite a jump however the energy dissipated only raises the coils temperature by around 0.20C. Looks like there's plenty of room for more power!
|
|