|
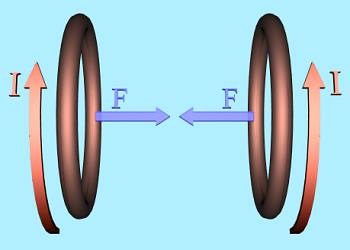
Coilgun Fundamentals 1,2 6. Projectile Saturation Before we discuss the effect of saturation we need to define what we mean by saturation. Put simply, saturation is a state in which the specimen has reached maximum magnetisation. Now magnetisation can be thought of as the amount of microscopic atomic dipoles which are aligned with one another. If we apply an external field these dipoles will tend to align themselves with this field. The stronger the external field becomes, the more dipoles become aligned. When all the dipoles are aligned the specimen is said to be saturated. This is a simplified description but it conveys the general idea. Now we need to ask ourselves what is the cause of the attraction between the coil and projectile. Ultimately the forces are due to charge motion; we have the motion of charge in the coil - the coil current, and we have orbital electron motion in the specimen - the dipoles. If you open any textbook on electromagnetism you'll find a description of the force between two infinite parallel current carrying wires. The force between these wires will be attractive if the currents are parallel and repulsive if the currents are anti-parallel. Now imagine two loops of wire sitting side by side as shown in fig 1 below.
Fig 6.1 Current carrying loops are mutually attracted
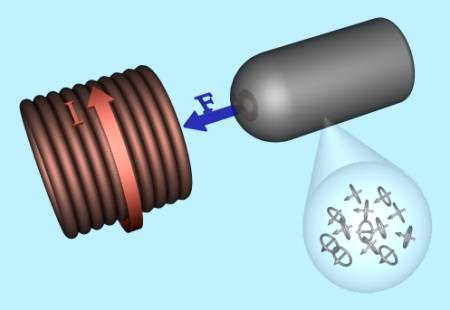
If the wire currents are in the same direction the force is attractive. Now the force between these loops will depend on their diameter, their respective current, and their separation, as well as the medium in which they are placed (e.g. free space). What is of interest to us is the fact that increasing the current in either loop will increase the force. Let's think of the coil and projectile. The coil is basically a large number of wire loops, each carrying the same current. The projectile is composed of many tiny current loops - the orbital electrons. Now normally in an unmagnetised ferromagnetic material the current loops are organised into small groups called domains. These domains are orientated in random directions so that macroscopically, the material exhibits no magnetisation. Fig 2 illustrates the randomly aligned loops. When an external field is applied, the loops within the domains experience a torque force which tries to align them with the field. This means that domains which are originally more aligned with the field tend to grow at the expense of the less well aligned domains - the better aligned domains 'hijack' loops from the surrounding less well aligned ones. The stronger the external field becomes, the more fully aligned the loops become.
Fig 6.2 An unmagnetised material contains randomly ordered magnetic dipoles
Fig 3 shows some alignment of the loops as the coil field begins to influence them. As the coil field is increased, more and more of the loops align until we reach a point where, for our purposes, all the loops become aligned i.e. the material is saturated. Think about the two loops in the first diagram again, we'll call the loop on the left the coil, and the one on the right the projectile. You can think of the saturation of the projectile as the right hand loop reaching a maximum current, but the force depends on the current in both loops. Since the current can be increased in the left hand loop (the coil) the attractive force will increase even though the projectile is saturated (right hand loop current fixed).
Fig 6.3 An external field causes alignment of the dipoles and an attractive force developes
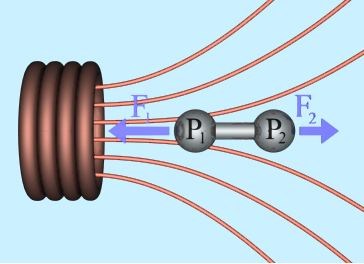
IMHO saturation of the projectile is of limited consequence, insofar as it doesn't place a limit on the attractive force. I do think that running a coilgun with a saturated projectile will be less efficient. There is another way to think about this using the pole concept of magnetics. Basically a projectile can be thought of as one big dipole which has maximum pole strengths determined by its saturation magnetisation. A magnetic pole (fictitious - nobody has found an isolated pole, although particle theory predicts their existence) experiences a force when placed in a magnetic field. Now since the projectile is a dipole it has two poles of opposite magnitude, so if it is placed in a magnetic field each pole will experience a force depending on the field strength around it and the 'sign' of the pole (+north / -south). Since the sign of the pole determines the direction of the force we find that the front of the projectile is attracted towards the centre of the coil and the end of the projectile is repelled from the coil. While this doesn't actually happen in reality, the use of poles is a valid concept. Here is the important point: the field is stronger towards the centre of the coil so the front pole experiences an attractive force which is stronger than the repulsive force generated by the rear pole, resulting in a net attraction. Now I mentioned earlier that the saturated projectile is a dipole of fixed maximum strength, however, since the coil field can still be strengthened by increasing its current the attractive force can still be increased. The strengthening of the coil field increases the difference in the force on the projectile poles and so increases the net attractive force. As fig 4 shows, any dipole which is placed in a field gradient will experience a net force, the larger the gradient becomes the stronger the resulting force. The forces on the poles can be expressed mathematically as:
where P is the pole strength. Since our projectile consists of two opposing poles in different field strengths, we can write
Now if we assume that the poles are of equal magnitude this reduces to
Fig 6.4. A dipole experiences a net force in a field gradient.
Something else to bear in mind is that although a material is often quoted with a value of saturation flux density this doesn't mean that the flux density is limited to this value. If the field is increased around a saturated material the flux density will continue to increase with a dB/dH equal to vacuum. The reason for this is that the material is full of space! - the space still contributes to the flux with a relative permeability of 1. This is important when using B-H curves for finite element analyses since the correct dB/dH must be used for large values of field beyond the materials saturation point. Summary From this simple interpretation of the nature of saturation and the realisation of the underlying cause of the attractive force, it would appear that the output from a coilgun can be increased when running with a saturated projectile. The problem is that although the force becomes proportional to the field ( and hence current) when the projectile is saturated, the energy required to establish a given field increases as the square of the current. In order to double the force it requires four times the energy to be supplied to the coil field. These diminishing returns make it clear that there will be practical limits to fields in reluctance coilguns, albeit fuzzy ones. You can find a description of magnetism from the perspective of poles in 'Introduction to Electromagnetism' by Martin Sibley.
|