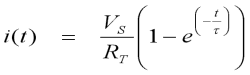Inductance Measuring Technique

It's possible to measure the self inductance of a circuit using a transient technique. This technique uses the exponential current transient to determine the time constant and hence inductance of the coil. While this method can readily provide inductance information about a circuit it does require the use of a digital storage oscilloscope or graphical multimeter. Some of the more advanced multimeters have an inductance measuring facility but if you are serious about investigating and designing coilguns then a good quality DSO should be a high priority on your shopping list. This article describes how to determine the coil's inductance from a trace of its current transient.

In order to accurately determine the inductance it is necessary to know the circuit resistance to a reasonable accuracy of say +/- 5%. This is not necessarily easy since the total circuit resistance is usually around 1 or less. Most multimeters only have a resolution of 0.1 and a dedicated ohmmeter is an expensive piece of kit. It is possible to get around this problem by introducing a much larger series resistance into the circuit. For a circuit with an estimated resistance of 1 the additional resistance can be say 100. This resistance then becomes the dominant resistance and we can ignore the resistance of the rest of the circuit. Since the coil is by far the largest inductive component we can solve for this inductance using the following method.

Fig 1 shows the main parameters of this inductive circuit. The transient response to a step voltage is governed by the time constant of the circuit and follows an exponential growth according to the function:

Eqn 1

The time constant is defined as

Eqn 2

where L and R are the circuit inductance and resistance respectively.

An important feature of this type of exponential growth is that there are almost exactly 5 time constant periods from the application of the step voltage until the current stablises. What we are interested in is the period of the time constant. This is best determined over the initial part of the exponential curve since it yields a more accurate result. In fact we are only going to consider the very first time constant period. If we solve the exponential current equation above for the first time constant period (t /= 1) then we find that i = 63.2% of maximum. Therefore to find all we need to do is find the time value corresponding to the current at 63.2% of maximum. The trace below is from Test Coil A using a 100 series resistor and a step voltage of 10V.

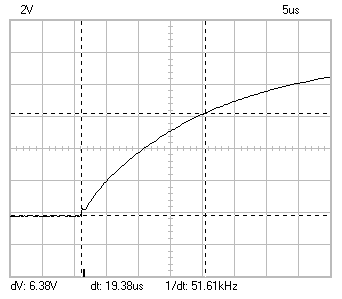
Fig 1

Notice that the voltage markers (horizontal dotted lines) are set to a dV of 6.38V which is 63.8% of the applied 10V. This is the closest value which could be set. The timebase markers (vertical dotted lines) are set to intersect the transient at the points where the voltage markers cut the curve. The resulting dt gives us the time constant for the circuit, in this case it's 19.38us. I typically work with 3 significant figures unless the calculations or experiments demand more. So now we have R=100 and =19.38us therefore the inductance of the circuit is 1.94mH. Since the coil inductance is the dominant inductance then we can say that the coil has an inductance of 1.94mH. It should be remembered that the coil inductance is frequency dependent, so different series resistor values will yield different results. An alternative method of calculating the coil inductance using FEMM is presented here.