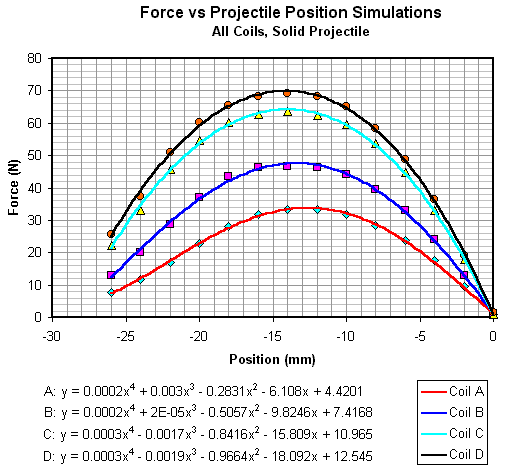
Open Loop Pulse Triggering Results

Coil Comparison

In this section we'll look at how the coils compare in various ways. The first thing we can consider is how the coils perform compared to simulated results. Fig 1 shows the force-position curves for the four coils using a solid projectile. 4th order polynomial trend lines are fitted to the data points. The equations can be integrated to determine the energy transferred to the projectile, these can then be used to calculate the speeds. Alternatively the data points can be imported into Matlab and numerically integrated.

 

Fig 1. Force - Position curves for solid projectile

 

It's important to choose the correct material when running a simulation, the results can vary significantly even with similarly sounding materials. I ran these simulations with 1006 steel which is a low carbon steel and should (I hope) be similar to the mild steel I'm using in its magnetic properties. Table 1 below shows the measured and simulated data.

 

Coil
A Sim
A Real
B Sim
B Real
C Sim
C Real
D Sim
D Real
Kinetic Energy (mJ)
587
298
859
506
1206
704
1323
802
Projectile Speed (m/s)
9.6
6.8
11.6
8.9
13.8
10.5
14.4
11.2

Table 1.

There is clearly a large difference in the simulated and measured data, although they agree better than I expected. Five possibilities come to mind as reasons for these discrepancies:

  • The 1006 steel material is a poor match for the actual projectile material.

  • The actual current curve is dynamic whereas the simulation uses a constant current.

  • The projectile drives some eddy currents in the accelerator tube and so gains less energy.

  • The projectile is retarded by the commutating current and loses energy.

  • Friction reduces the energy transfer to the projectile.

These are the most obvious factors but there are probably others. I would say that the commutating current interaction is probably the most significant with accelerator tube eddy currents coming second. The rising edge of the current pulse probably isn't that influential because the projectile is going slowly to begin with so the current reaches its maximum before the projectile moves very far.

In the theory section I derived an equation which can be used to determine the wire diameter which will give the maximum current density for a given set of coil dimensions and circuit resistance. If we put the typical test coil dimensions into this equation and specify an RE of 0.08 we get a optimal wire diameter of 1.57mm. This is really close to the wire used in coil D which also is the best performer in terms of muzzle speed. There isn't much point in plotting the current density vs wire diameter without more data points. I may make up additional coils with larger wire diameters to try and establish the actual optimal diameter.

 

 

 

  
Results Coil DTop