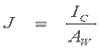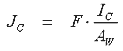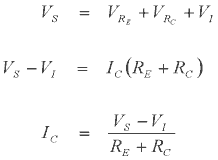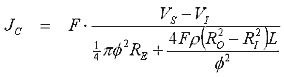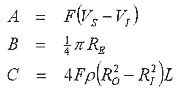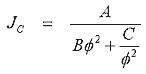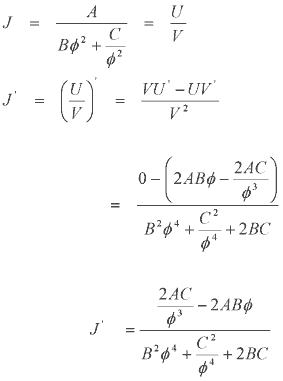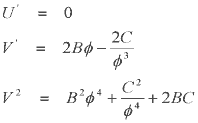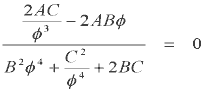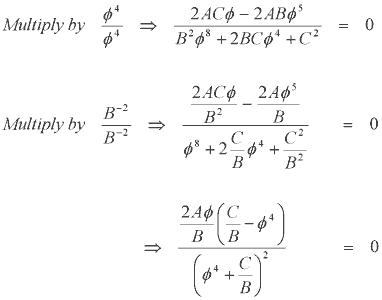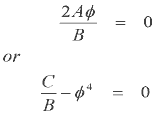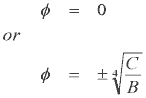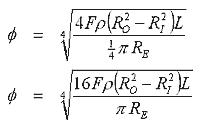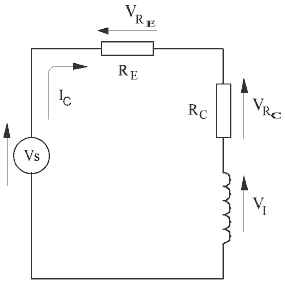
Optimising Current Density

1,2,3

It is possible to determine a wire diameter for a given coil geometry which will maximise the current density in the coil. First we need to look at the circuit as shown below -

Fig 1

R_E is the external resistance (absolutely everything except the coil), R_C is the coil resistance, VI is the induced voltage in the coil and Vs is the source voltage. It is important to include source internal resistance and switching device resistance when calculating RE. We'll keep things managable and concentrate on the steady state condition so we can ignore Vs and VI as variables. First let's define the current density J -

Eqn 1

where Ic is the current in the wire and Aw is the wire cross-sectional area.

The current density in the coil is then

Eqn 2

where F is the filling factor.

Applying Kirchhoff's voltage law around the loop produces the following relationship -

Eqn 3

Static Current Analysis

Now if we substitute the coil resistance equation and eqn 3 above into eqn 2 we get -

Eqn 4

This is getting a bit messy so I'll lump together some of the constants -

giving us -

Eqn 5

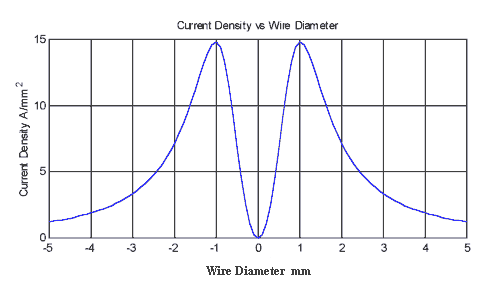
This is a fairly simple function and if we plot J against we get the following general curve -

Fig 2

Obviously only the +ve values of wire diameter have any meaning. This is quite revealing since it shows that there is a certain value of (for a given coil geometry) which will yield the maximum current density.

Let's take the final step and tie down an expression which will give the wire diameter for maximum current density without having to plot the whole function. If we differentiate J we can get values for the turning points of the function. Using the Quotient Rule gives us -

Eqn 6

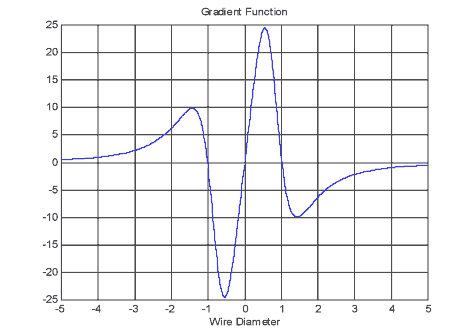
The differentiated function looks like this -

Fig 3

It clearly has three roots and these can be found by equating J' = 0 -

Eqn 7

Now apply some math manipulation -

Eqn 8

The expression we get above can now give us the roots. The numerator yields two expressions for the roots-

Solving for these -

Eqn 9

Only the positive root is of interest. Now we can substitute for the constants C and B as defined earlier to give -

Eqn 10

The wire diameter given by this expression is a good starting point from which to begin experimentation. Keep in mind that the parameters which you use need to be reasonably accurate for the calculation to give meaningful results. In particular you'll need to produce an accurate value for the R_E. Whether you do this by calculation or from measurement is up to you. One crucial aspect missing from this analysis is the induced voltage term. Future analysis will concentrate on developing an expression for optimised current density under dynamic conditions.