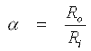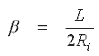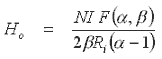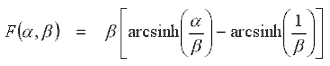|
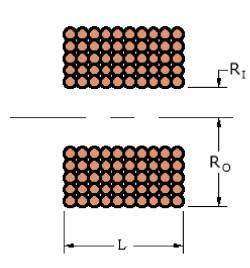
Optimised Coil Geometry Let's look at how the thickness of the coil affects the field strength at its centre. The basic coil parameters are illustrated below.
Fig 1
Firstly let's define some basic geometrical relationships
It can be shown that the field, Ho, at the centre of the solenoid is
where N is the number of turns, I is the coil current, and F(a,b) is the 'field factor' defined as
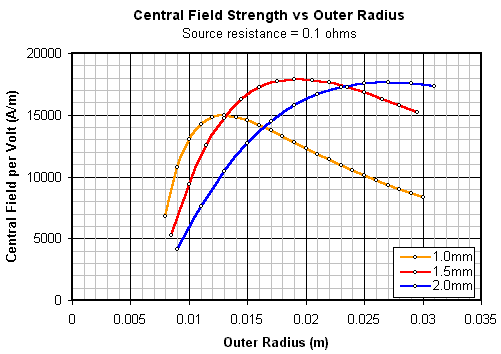
We can use these equations in conjunction with the coil resistance equation to plot Ho as a function of Ro for any combination of L, Ri and wire diameter. Fig 2 shows the field strength for three different wire diameters using a coil with L=26mm and Ri=7mm.
Fig 2. Field strength vs outer radius for various wire diameters
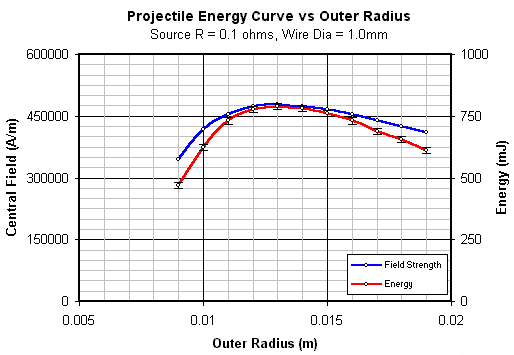
The field strength plots are based on a source of 1V. The particular voltage level doesn't matter, we're only interested in the relative effect of wire diameter and outer radius. It's obvious that for any given wire diameter there is an optimal outer radius which maximises the field strength. Why do we want to maximise the field strength? Well the central field strength is probably the most important factor governing the muzzle energy of the projectile. Need some convincing? Fig 3 shows the results of a simple experiment which involved measuring the muzzle speed from a coil with varying values of outer radius. Coil B (1mm wire) was used for this. As each speed measurement was completed a layer of was removed until the coil was 2 layers thick. 'Suckback' is reduced by using the multidiode commutation arrangement. The projectile energy is plotted along with the calculated central field strength.
Fig 3. Correlation between central field and projectile energy.
There is a good degree of correlation between the energy and the central field. Perhaps the most notable aspect of these curves is that the peak energy and peak field occur at the same coil outer radius. The correlation between these peaks is very striking and reflects the likelyhood that central field strength will play a key role in determining the best coil geometry. It's perhaps worth commenting on the fact that there isn't a 1:1 correspondence on all points of the curve. The first thing that comes to mind is the source resistance value. This is based on the battery source internal resistance, the mosfet module resistance, the current sensor resistance and the wiring resistance. Apart from the current sensor none of these resistances are known to a high degree of accuracy so the absolute magnitudes of Ho could be off by some amount. Another reason could simply be that the the field strengths involved in this experiment are insufficient to induce saturation magnetisation in the projectile so it is still subject to the nonlinear portion of its B-H curve. There's also suckback acting as an uncontrolled factor which will no doubt vary with the changes in coil radius. I suspect that running a similar experiment with a higher currents, and hence field strengths, will produce a tighter correlation. This experiment is by no means definitive, additional experiments need to be run with a selection of 'base geometries' - length and inner radius combinations - in order to determine if the outer radius can be confidently specified using the peak Ho. Also, the Ho analysis is based on the pulse width being at least 6 time constants - steady state approximation. The Coil B configurations satisfied this limitation but obviously not all coils will. Some type of dynamic factor is required to refine the Ho analysis. One last point, if you examine the 1.5mm wire curve in fig 2 you'll notice that a coil using this wire diameter has a peak field when Ro is 19 mm. This peak is significantly larger than the 1.0mm peak so does a coil based on this geometry perform better? We can answer this by looking at Coil D since it more or less conforms to these dimensions. From previous experiments using identical multidiode commutation we can see that Coil D produces a muzzle energy of about 970mJ which is obviously larger than the 790mJ maximum generated by the 1mm wire. If we calculate the energy ratio and field ratio we get 1.23 and 1.20 respectively.
Sources:
|